これ丸善出版 ISBN 978-4^621-08580-6 C 3042)を購入し、読み始めて数ヶ月、まだ終わらない(たぶん 終わることはない)ので、復習というか忘備録というか、整理というか、記録していくことにしようと思う。
きっかけは筑波大学薮野先生の特別講演であった。ストロガッツと薮野先生との関係は、小職浅学のため存じ上げないが、あまりにも今まで、相空間、例えば単純な一自由度系のばね、マス、ダンパー系の2次微分方程式で表現される系であれば、変位と速度を横軸と縦軸にとり、応答の軌跡を示すことをしていなかったと気づいたことによる。下図は横軸変位、縦軸速度で初期変位を0.5として解析した結果である。SCILABによる。その下の図は同じ解析の時系列グラフである。

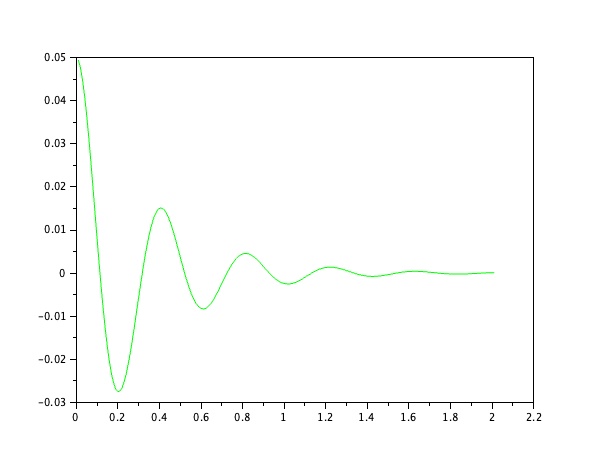
時系列データは、直感的に振動の様子がわかるので、これだけで十分であるのだが、非線形となった場合には相を見ることが重要になる。また、減衰の選定においても相空間で考えることが、減衰を検討する上で重要になってくるのではないかという期待から、この図書を勉強するようになっている。
以上は線形であったが、例えばvan der Pol方程式の振動現象は非線形な減衰を含んでいる振動となりそのパラメータμ=1.5とした例では以下のようになる。
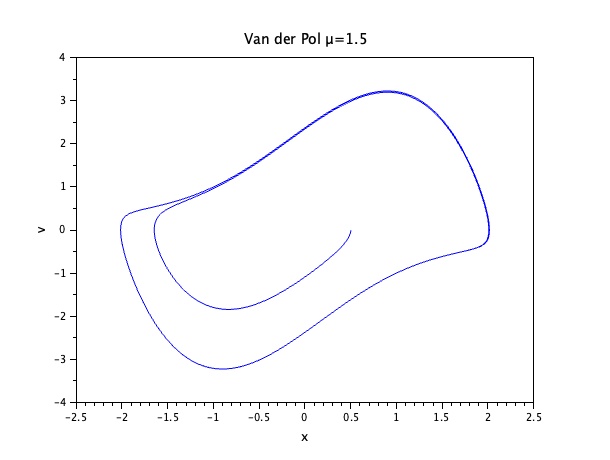
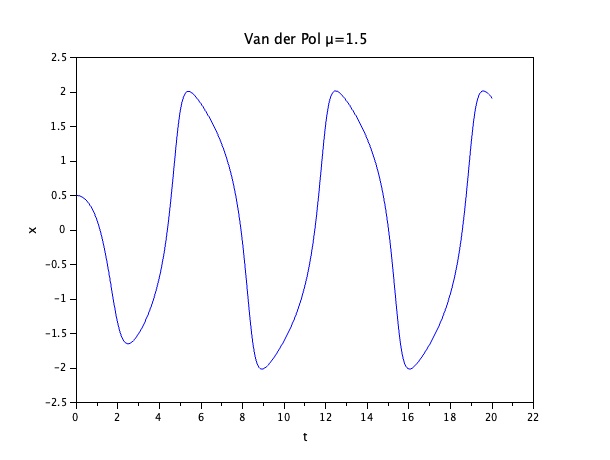
式は以下となる。
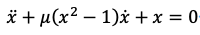



コメント